https://github.com/lovedlim/bigdata_analyst_cert/blob/main/part3/ch3/ch3_chi_square.ipynb
T 검정
- stats.ttest_1samp
- stats.ttest_rel
- stats.ttest_ind
from scipy import stats
# 단일표본
t_statistic, p_value = stats.ttest_1samp(data, popmean, alternative)
print(t_statistic, p_value)
# 대응표본 ** 문제에 따라 a,b 입력 순서에 따라 alternative설정이 'greater,less,two-sided')
t_statistic, p_value = stats.ttest_rel(data_a, data_b, alternative)
# 독립표본
t_statistic, p_value = stats.ttest_ind(data_a, data_b, alternative)카이제곱 검정 (기출N회)
- 학습 우선순위 : 독립성/동질성검정 > 적합도 검정
- 카이제곱은 크게 적합도 검정, 독립성 검정, 동질성 검정 3가지 종류가 있음
- 이 중, 독립성 검정과 동질성 검정은 검정이 chi2_squred 검정으로 코드 및 해석방법이 동일하며
- 독립성/동질성 검정은 문제를 읽고 교차표 만드는 것이 핵심 (적합도 검정 제외)
from scipy.stats import chi2_contingency, chisquare
print(chi2_contingency(df))
print(chisquare(observed, expected)) #관기
#1 독립성/동질성 검정 : 교차표는 문제 읽고 df 만들어서 아래 코드 두줄 입력하면 끝
from scipy.stats import chi2_contingency()
print(chi2_contingency(df))
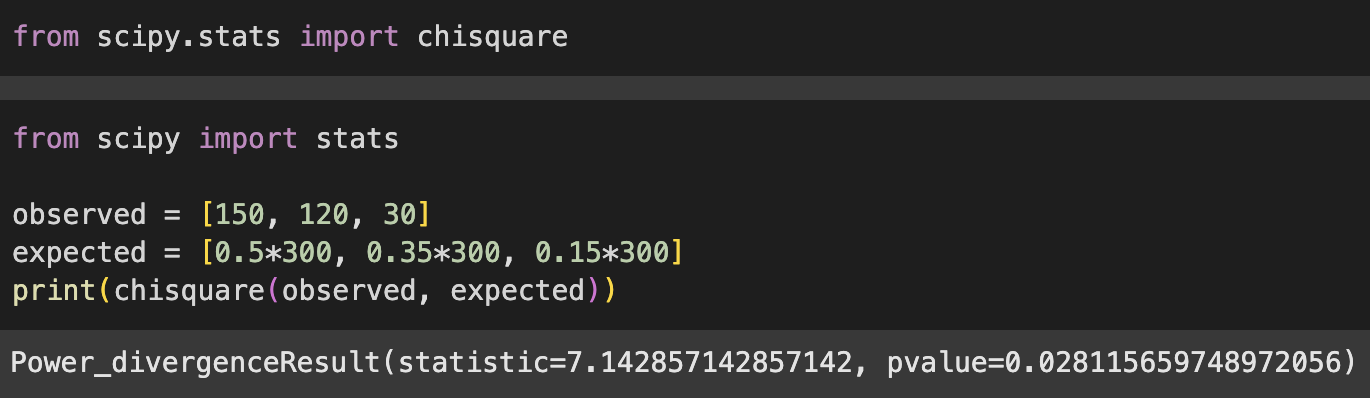
#2 적합도 검정 : 관측값, 기대빈도값 - 빅데이터분석기사 6회 기출 관.기
from scipy.stats import chisquare
print(chisquare(observed, expected)독립성 검정 : 2개의 변수가 서로가 독립적인지, 연관성 있는지 검정
예제 - 성별에 따라 운동을 좋아하는지 조사한 결과다. 성별과 운동 선호도가 독립적인지 가설검정을 실시하시오.
- H0 : 성별과 운동 선호도는 독립적이다. (연관성 없다)
- H1 : 성별과 운동 선호도는 독립적이지 않다. (연관성 있다)

# 독립성 검정 - 2개의 변수(x1,x2)가 서로 독립적인지 연관성 있는지 검정 - 교차표 생성
# 0. 임포트
from scipy.stats import chi2_contingency
# 1. 교차표 생성
# 1.1 교차표 생성 - cross tab 이용 (raw data 주어졌을 때)
df=pd.crosstab(df['x1'],df['x2'])
# 1.2 교차표 생성 - 리스트만 작성 (인덱스, 컬럼 생략) **시험에서는 리스트만 만들자**
df = [[80, 30], [90, 10]]
# 1.3 교차표 생성 - pd.DataFrame으로 생성 (인덱스, 컬럼 이름 지정)
df = pd.DataFrame([[80, 30], [90, 10]],
columns=['좋아함','좋아하지 않음'],
index=['남자', '여자'])
# 2. 독립성 검정
print(chi2_contingency(df))
독립성 검정 결과 해석 예시
- 첫번째 값은statistic(검정결과), 두번째 값은 p-value값이 출력된다.
- 아래에서는 pvalue가 0.0026으로 유의수준 5%하에 0.05미만으로 귀무가설을 기각하고, 대립가설 즉 두 변수간의 상관성이 있다고 판단한다.

동질성 검정 : 2개 이상의 집단에서 분산의 동질성을 가졌는지 검정
예제 - 학과에 따라 학교 공식 동아리에 가입한 학생의 수와 가입하지 않은 학생의 수를 비교하는 동질성 검사를 실시하고, 검정 결과를 작성하시오.
- H0 : 모든 그룹의 분포나 비율은 동일하다
- H1 : 각 그룹의 분포나 비율은 동일하지 않다.

# 동질성 검정 - 서로 다른 그룹 또는 모집단이 동일한 범주 분포를 갖는지 검정
# 0. 임포트
from scipy.stats import chi2_contingency
# 1. 교차표 생성
from scipy.stats import chi2_contingency
# 1.1 교차표 생성 - cross tab 이용 (raw data 주어졌을 때)
df = pd.crosstab(df['학과'], df['동아리가입여부'])
# 1.2 교차표 생성 - 리스트만 작성 (인덱스, 컬럼 생략) ** 시험에서는 간단하게 리스트만 만들자 **
df = pd.DataFrame([[50, 50], [30, 70]])
# 1.3 교차표 생성 - pd.DataFrame으로 생성 (인덱스, 컬럼 이름 지정)
df = pd.DataFrame([[80, 30], [90, 10]],
columns=['좋아함','좋아하지 않음'],
index=['남자', '여자'])
# 2. 독립성 검정
print(chi2_contingency(df))
동질성 검사 해석 예시
- 첫번째 값은 검정통계량 값, 두번째 값은 p-value값
- 첫번째 값은statistic(검정결과), 두번째 값은 p-value값이 출력된다.
- 아래에서는 pvalue가 0.006098으로 유의수준 5%하에 0.05미만으로 귀무가설을 기각하고, 대립가설 즉 두 학과의 동아리 가입 비율이 동일하지 않다고 판단한다.

적합도 검정
'자격증 > 빅데이터분석기사-실기' 카테고리의 다른 글
| 빅데이터분석기사 실기 - 체험환경 사이트 / help(), dir() 활용하기 (0) | 2024.11.24 |
|---|---|
| 빅데이터분석기사 실기 1유형 (0) | 2024.11.24 |
| 빅데이터분석기사 실기 3유형 - 회귀분석/로지스틱회귀분석 (0) | 2024.11.17 |
| 빅데이터분석기사 실기 2유형 (마스터코드) (0) | 2024.11.16 |
| 빅데이터분석기사 실기 3유형 - T검정 (0) | 2024.11.15 |


